1、说明
2010年的一篇论文,说明深度神经网络为什么难以训练,当时只讨论了Sigmoid,tanh和Softsign激活函数- 提出了一种初始化权重weights的方法,能够解决训练中梯度消失的问题
- 但是使用现在的
ReLu激活函数,同样使用此初始化方法就会出现问题。
- 但是使用现在的
2、Sigmoid激励函数实验
- 说明
- 论文首先通过实验观察激活函数的影响,指出
Sigmoid函数是不适合作为深度神经网络激活函数的 - 因为它的均值总是大于0的,如下图,导致后面的隐藏层
hidden layer趋于饱和,并且发现饱和的神经元可以自发移出饱和趋于,但是非常慢。接着发现一个新的非线性的激活函数是非常有益的。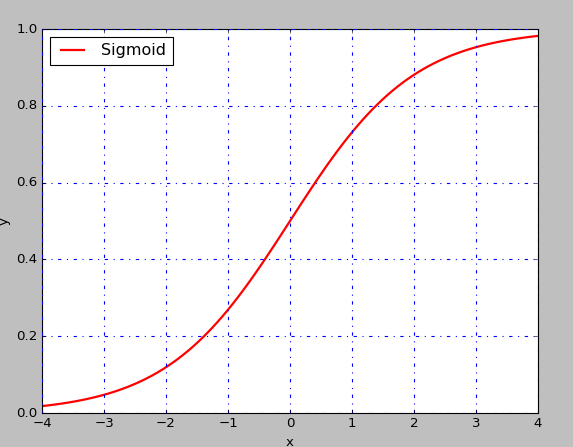
- 最后观察每一层激活值和梯度的变化,给出了一种新的初始化权重的方法。
- 论文首先通过实验观察激活函数的影响,指出
- 实验部分
- 初始化偏置
biases为0,权重w服从均匀分布,即:
$${{W_{ij}} \sim U[ - {1 \over {\sqrt n }},{1 \over {\sqrt n }}]}$$ - 其中
n为前一层的神经元个数。然后构建了一个含有4个隐含层的神经网络,激活函数使用的是Sigmoid - 观察每一层的激活值的均值和标准差随着训练次数的变化,
layer1表示第一个隐含层的输出,以此类推。如图所示:实线表示均值mean value,垂直的条表示标准差。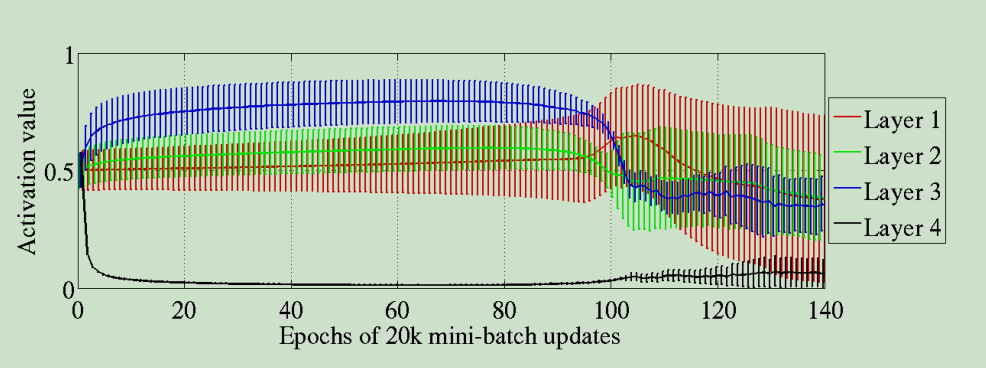
- 初始化偏置
- 实验的直观理解
- 最后我们使用 ${Softmax(b+Wh)}$ 作为输出预测的,刚开始训练的时候不能够很好的预测
y的值,因此误差梯度会迫使Wh趋于0,所以会是h的值趋于0,h就是上一层的输出,所以激活值很快为0。 - 但是对于
tanh函数是关于原点对称的,图像如下,值趋于0是好的,因为梯度能够反向传播回去,但是对于sigmoid函数来说就趋于饱和的位置了,梯度很难反向传回去,也就学习不到东西了。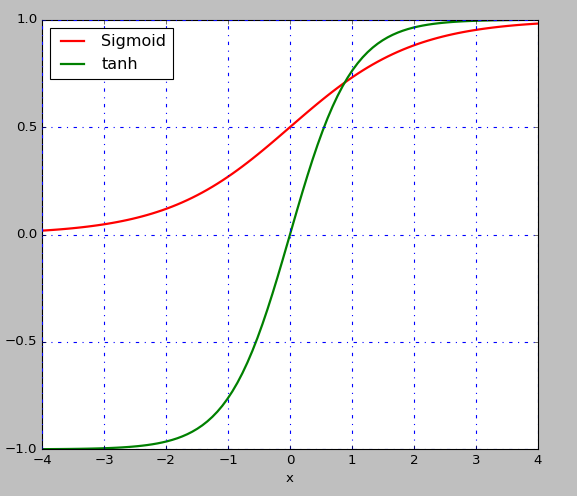
- 最后我们使用 ${Softmax(b+Wh)}$ 作为输出预测的,刚开始训练的时候不能够很好的预测
3、梯度计算和公式推导
1) 代价函数
- 代价函数使用的是交叉熵代价函数,相比对于二次代价函数会更好
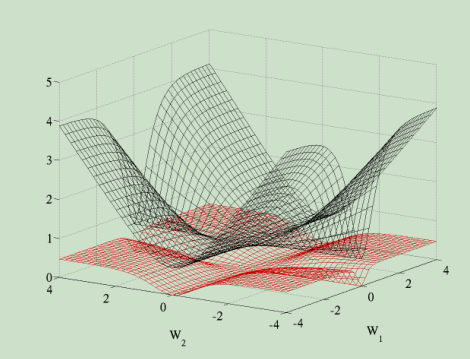
- 二次代价函数较为平坦,所以使用梯度下降会比较慢。
2) 公式推导
- 符号说明
${z^i}$………………………………第i层的激活值向量
${s^i}$………………………………第i+1层的输入
$X$………………………………输入
${n_i}$………………………………第i层神经元个数
$W$………………………………权重 - 可以得到:
$${s^i = {z^i}{W^i} + {b^i}}$$
$${z^{i + 1} = f({s^i})}$$ - 所以分别对上面两式求偏导可以得到:
$${{\partial Cost \over \partial s_k^i}=f^{'}W_{k,\bullet}^{i+1}}{ \partial Cost \over \partial s^{i+1}}…………………………….(1)$$
$${{\partial Cost \over \partial w_{l,k}^i} = z_l^i}{\partial Cost \over \partial s_k^i}........................................(2)$$ 推导如下 ![BP推导][5] - 上面公式推导说明 - 其中 $${{\partial Cost \over \partial s^{i-1}}={\delta ^{i-1}}}$$
- 这里
W从1开始,上面给出的最终公式是从0开始。 - 对权重的偏导(梯度)再乘以输入 ${z^i}$ 即可。
- 因为我们使用均匀分布进行初始化,所以方差是一样的,对于
tanh函数的导数,$${[\tanh (x)]^{‘}} = 1 - {[\tanh (x)]^2}$$ - 所以:$${f^,}(s_k^i) \approx 1$$
- 实际这里作者假设了这个区间内激活函数是线性的,第二篇论文中也有提到。(下面会给出)
- 根据方差的公式: $$Var(x) = E({x^2}) - {E^2}(x)$$
可以得到: $${Var[z^i] = Var[x] \prod\limits_{j=0}^{i-1}n_j Var[W^j]}…………………………(3)$$
推导如下:
- ${Var(s) = Var(\sum\limits_i^n w_i x_i)}=\sum\limits_i^n Var(w_ix_i)$
- ${Var(wx) = E(w^2x^2) - E^2(wx)} \\
\quad\quad\quad\quad=E(w^2)E(x^2) - E^2(w)E^2(x) \\
\quad\quad\quad\quad=[E(w^2)-E^2(w)][E(x^2)-E^2(x)] + E^2(w)[E(x^2)-E^2(x)] + E^2(x)[E(w^2)-E^2(w)] \\
\quad\quad\quad\quad=Var(w)Var(x)+E^2Var(x)+E^2Var(w)$ - 因为输入的均值为0,所以$${E(w) = E(x) = 0}$$
- 所以:$${Var(wx) = Var(w)Var(x)}$$
- 又因为${f^{‘}(s_k^i) \approx 1}$成立,然后代入上面的式子即可
- 根据公式(1),所以对${S^i}$偏导数的方差为:$${Var[{\partial Cost \over \partial s^i}]} = {Var[{\partial Cost \over \partial s^n}]}{\prod\limits_{j=i}^n}{n_{j+1}Var[W^j]}$$
根据公式(2),代入到对权重
w偏导(即为梯度)的方差为: $${Var[{\partial Cost \over \partial w^i}]} = {\prod \limits_{j=0}^{i-1} n_j Var[W^j]}{\prod \limits_{j=i}^{n-1} n_{j+1}Var[W^j] \ast Var[x] Var[{\partial Cost \over \partial s^n}]}$$对于正向传播,希望:$$\forall (i,j),Var[{z^i}] = Var[{z^j}]$$
- 从反向传播的角度同样可以有:$${\forall (i,j), Var[{\partial Cost \over \partial s^i}]} = Var[{\partial Cost \over \partial s^j}]$$
- 就可以转化为:$$\left\{ {\matrix{
{n_iVar[w^i]}=1 \cr
{n_{i+1}Var[w^i]}=1 \cr
} }…………………………(4) \right.$$- 比如第一种(公式(3)): $${Var[z^i] = Var[x] \prod\limits_{j=0}^{i-1}n_j Var[W^j]}$$ $$Var(z^i) = Var(x)$$
- 所以${n_i}Var[{w^i}] = 1$ ,第二种情况同理
- 所以将 (4) 中的两式相加可得:$${Var[{W^i}]}={2 \over {n_i + n_{i+1}}}$$
- 如果所有层的神经元个数一样时:$$\left\{ {\matrix{
{Var[{\partial Cost \over \partial s^i}] = [nVar[W]]^{d-i}Var[x]} \cr
{Var[{\partial Cost \over \partial w^i}] = [nVar[w]]^{d}Var[x]Var[{\partial Cost \over \partial w^n}]} \cr
}} \right.$$ - 可以看到,所有层的梯度的方差都是一样的。但是对于很深层的神经网络还是有可能导致梯度消失。
- 如果所有层的神经元个数一样时:$$\left\{ {\matrix{
4、初始化权重方法
- 最后提出了一个归一化的初始化方法,因为
W服从均匀分布,根据均匀分布的方差公式可以得到:$${[c-(-c)]^2 \over 12} = {c^2 \over 3}$$ - 所以得到:$${2 \over {n_i + n_{i+1}} =}{ c^2 \over 3}$$
- 求出:
- 所以最终给出初始化权重的方法为:$${W \sim U[-{{\sqrt 6}\over {\sqrt n_i+n_{i+1}}},{\sqrt 6 \over \sqrt {n_i + n_{i+1}}}]}$$
5、总结
- 论文讨论了
Sigmoid,tanh激励函数权重初始化的问题,并给出了初始化的方法,- 但是针对ReLu这种激励函数是不适用的,第二篇会提到。 - 并且推导过程中假设了激励函数在初始化对应区间上是线性的,即假设导数恒为1我感觉也是存在问题的。
- 作者给出的实验部分网络的深度还是很有限的,随着网络的不断加深,对应的初始化权重的分布范围还是会不断减小的。可以通过控制学习率参数等方式来进行对应处理。
Reference
- 本文链接: http://lawlite.me/2016/12/20/论文记录-UnderstandingTheDifficultyOfTrainingDeepFeedforwardNeuralNetworks/
-
版权声明:
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 3.0 许可协议
 。转载请注明出处!
。转载请注明出处!

