1、概述

• 压缩主要分为三个阶段：剪枝(pruning)、训练分层(trained quantization)以及 哈夫曼编码(Huffman coding)
• 可以压缩35到49倍，并且不影响精度
• [模型压缩的主要用于还是能够用于小型的设备上，例如手机端等，比如Google的Mobile Net, 但是准确度肯定要比正常的电脑端训练的大网络低一些，在所难免]
• [一般的训练好的神经网络模型文件有几百兆的大小，比如Google预训练好的模型，计算量也很大，在手机端运行不太现实]

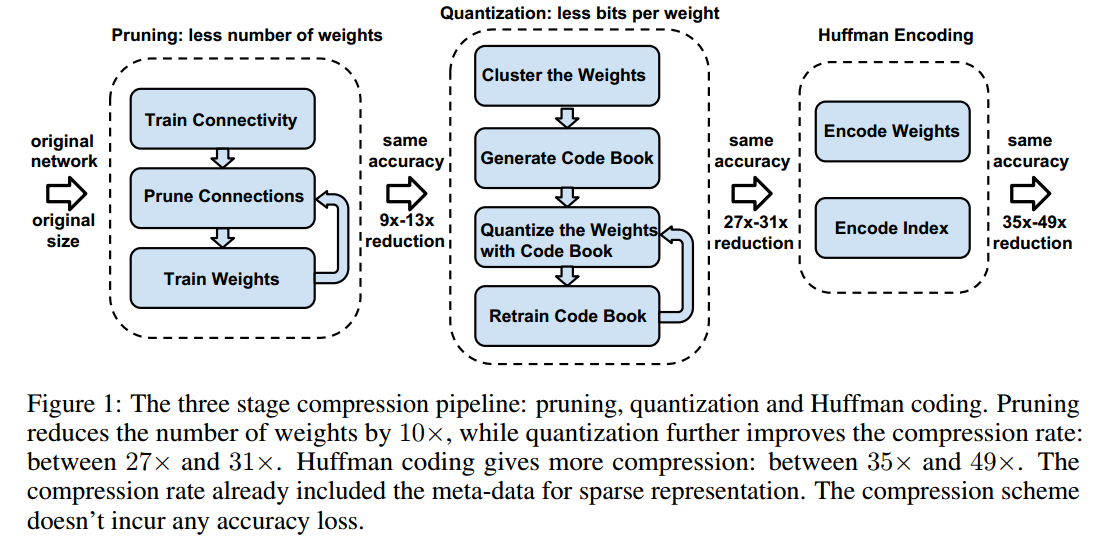
2、Pipline

• 剪枝可以压缩10倍左右，加上分层可以达到27到31倍，再加上哈夫曼编码可以达到35到49倍
  • 剪枝：去除多余的连接，比如权重非常小的连接
  • 分层：我感觉像是聚类，多个连接共享一个权重

3、剪枝

• 主要是删去权重值weight比较小的，(设置为0)，可以设置一个阈值(threshold)
• 所以权重矩阵变的比较稀疏，可以采用压缩行存储（Compressed Row Storage(CRS)）或列存储来存储稀疏矩阵
  • 主要包括3个数组，浮点值数组val，两个整形数组col_index, row_ptr
  • val(k) = a(i,j), col_index(k) = j
  • row_ptr是每行数据第一个非0元素在val中的索引，最后加上一位非0元素的个数，即row_ptr(n+1) = a+1
    • 比如
      

• 所以总共需要的大小为：2a+n+1
  • a为矩阵非零元素的个数
  • n为行数

4、训练分层量化

• 比如所有的权重聚成4类，cluster index表示每个权重对应的类别
• 梯度采用同一类别内进行累加，然后进行微调更新

• 假设有n个连接，每个连接的用b bits来表示，并假设有k个cluster, 只需要$log_2(k)$bits去表示索引，则压缩率可以为：$$r = {nb \over nlog_2(k)+kb}$$
  • nb即为没有聚类前总共需要的bits
  • $nlog_2(k)+kb$就是聚类索引的bits加上聚类后连接需要的bits
  • 比如上面的例子为：${1632 \over 162+4*32} = 3.2$

4.1 权值共享

• 使用k-means算法进行聚类，确定每一层共享的权重，在一个cluster中的权重共享，注意这里没有跨层
• 将$W={\{w_1, w_2, … ,w_n\}}$聚为$C={\{c_1,c_2, … ,c_k\}}$类, 其中n>>k
  • 优化函数为：$$\mathop {\arg \min }\limits_c \sum\limits_{i=1}^k \sum\limits_{w \in c_i} |w-c_i|^2$$

    4.2 共享权重的初始化方法（三种）

  • Forgy: 就是随机初始化方法初始化聚类的中心，如下图，因为权重分布有两个峰值，初始化的值都在峰值附近
  • 基于密度的初始化方法：如下图，先是根据累积分布函数(CDF)线性等分y轴，然后根据CDF找到对应的x轴的坐标，即为聚类的中心。（也是在峰值附近，和Forgy方法相比更分散一些）
  • 线性：就是根据权重的最小值和最大值等分，分散性最大

• 神经网络中一般权重值越大，它的作用也就越大，所以对于前两种初始化方法都是在峰值附近，也就意味着值少的地方很小的概率会被初始化，所以不太好，实验中线性初始化的效果最好（但是大权重值的是很少的）

4.3 前向和反向传播

• 计算时查表就可以了
• 反向传播用于更新聚类中心的权重值
  $${\partial L \over \partial C_k} = \sum\limits_{ij}{\partial L \over \partial W_{ij}} {\partial W_{ij} \over \partial C_k} = \sum\limits_{ij} {\partial L \over\partial W_{ij}}\Gamma (I_{ij}=k)$$
  • 其中L是损失函数，$C_k$是第k个聚类的中心
  • $I_{ij}$为聚类中心的索引，如下图，就是同一类别梯度求和
    

5、哈夫曼编码

• 就是按照聚类中心的出现的概率从大到小排序进行Huffman编码
• 根据上面的结果，权重大都分布在两个峰值附近，所以利于huffman编码

6、结果及讨论

• 没有准确度损失
  
• pruning 和 quantization 结合使用效果最好
  
• 和之前别人的工作的比较
  • SVD 压缩了模型但是精度损失较大

• 缺点就是在运行时现有的GPU不能进行间接的矩阵输入查找，以及相对索引 CSC 或 CSR, 还有剪枝的操作主要是在全连接层，但是计算量大的卷积层较少，虽然可以通过BLAS libraries或是specialized hardware进行加速，但是也是受限的（下篇Paper中也有提到）
• [我觉得剪枝和权值共享其实是能够防止过拟合的，所以准确度没有损失]
• [权值共享时是当前层的权值共享，不是整个网络的权值共享]

Reference

• https://arxiv.org/abs/1510.00149
• http://blog.csdn.net/bigpiglet_zju/article/details/20791881

赏

谢谢你请我吃糖果

支付宝

微信