R树索引


阅读数: 次   
× 文章目录
  1. 1. 前言
    1. 1.1. B树
  2. 2. R树介绍
  3. 3. R树数据结构
  4. 4. 代码实现
    1. 4.1. GeoTools实现
      1. 4.1.1. R树构建
      2. 4.1.2. 查询
    2. 4.2. GeoTools实现说明
      1. 4.2.1. STR算法
      2. 4.2.2. Insert
      3. 4.2.3. Build
      4. 4.2.4. Query
  5. 5. Reference

前言

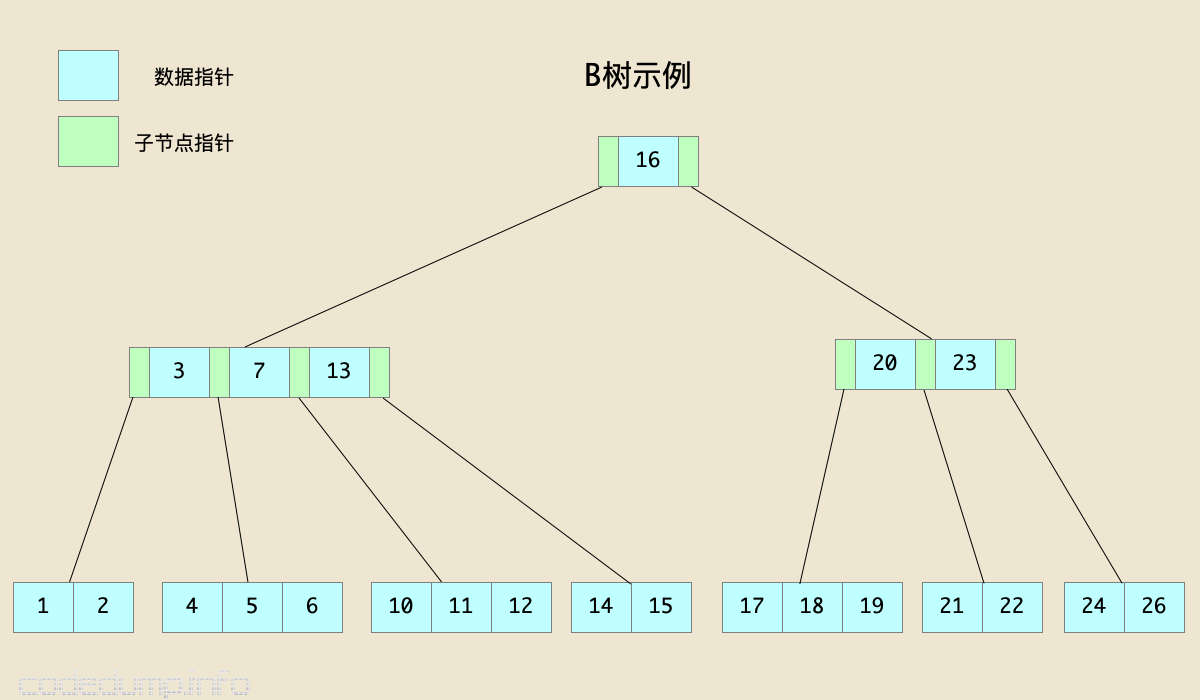
B树

  • B树是一棵平衡树，它是把一维直线分为若干段线段，当我们查找满足某个要求的点的时候，只要去查找它所属的线段即可。这种思想其实就是先找一个大的空间，再逐步缩小所要查找的空间，最终在一个自己设定的最小不可分空间内找出满足要求的解。

    img

    btree-example

R树介绍

  • 二维 R 树索引不同于传统的等级（一维）B 树索引。空间数据是二维的，所以无法使用 B 树索引组织空间数据。
  • 同样，使用 R 树索引不能表示非空间数据。R 树是一种用矩形表示结点的树状结构来组织数据的访问方法。

R树数据结构

  • R树是B树在高维空间的扩展，是一棵平衡树。
  • 每个R树的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。

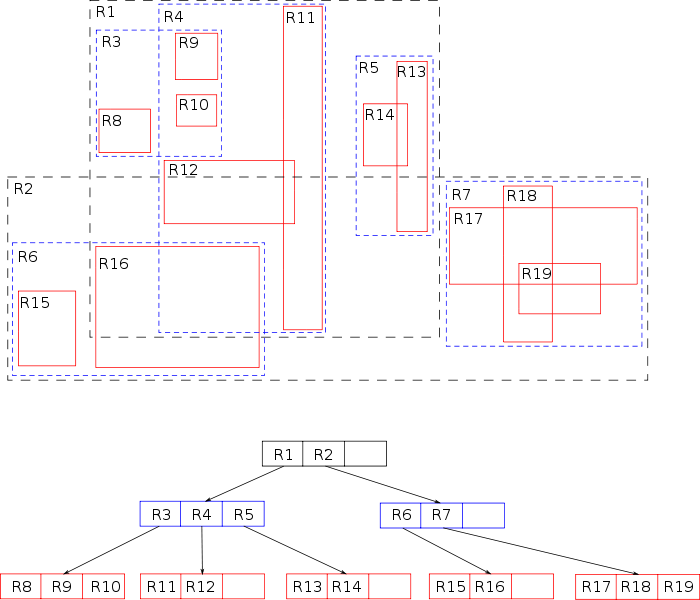
File:R-tree.svg

  • M 为一个节点中的最大条目数。取 m <= M/2，约定此 m 为一个节点中的最小条目数。此时，R 树具有如下性质：
    • 若叶节点不是根节点，则每个叶节点所包含的索引记录个数介于 m 与 M 之间；
    • 对于叶节点中的索引记录（I，tuple-identifier），I 是其最小外包矩形；
    • 若非叶节点不是根节点，则其中包含的子节点个数介于 m 与 M 之间；
    • 对于非叶节点中的条目（I，child-pointer），I 表示能够覆盖其所有子节点的外包矩形的外包矩形。
    • 根节点若非叶节点，则其至少有两个子节点。
    • 所有叶子节点都在同一层。

代码实现

GeoTools实现

R树构建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
UIManager.setLookAndFeel(UIManager.getCrossPlatformLookAndFeelClassName());
// 显示打开shp文件的窗口
File file = JFileDataStoreChooser.showOpenFile("shp", null);
if (file == null) {
  return;
}
STRtree stRtree = new STRtree();
FileDataStore store = FileDataStoreFinder.getDataStore(file);
SimpleFeatureSource featureSource = store.getFeatureSource();
SimpleFeatureCollection features = featureSource.getFeatures();
SimpleFeatureIterator featureIterator = features.features();
while (featureIterator.hasNext()) {
  SimpleFeature simpleFeature = featureIterator.next();
  Geometry geometry = (Geometry) simpleFeature.getDefaultGeometry();
  stRtree.insert(geometry.getEnvelopeInternal(), simpleFeature);
}
// 构建RTree
stRtree.build();

查询

1
2
3
4
5
// RTree查询
Envelope envelope = new Envelope(new Coordinate(10, 20));
List<?> result = stRtree.query(envelope);
System.out.println("query size: " + result.size());
result.forEach(System.out::println);

GeoTools实现说明

STR算法

  • geotools中R树的实现使用的是STR算法，
    • 对矩形的分组只考虑每个矩形的中心点，STR的基本思想是将所有的矩形分配到$\left \lceil r/n \right \rceil $（取上界）个分组中；
    • 首先，对矩形按x坐标排序，然后划分成 $\sqrt{r/n}$ 个slice；
    • 然后，对slice内的矩形按y坐标排序，进一步划分成 $\sqrt{r/n}$ 份；
    • 最后递归的向上构建，直到根节点。

image-20220327151016622

Insert

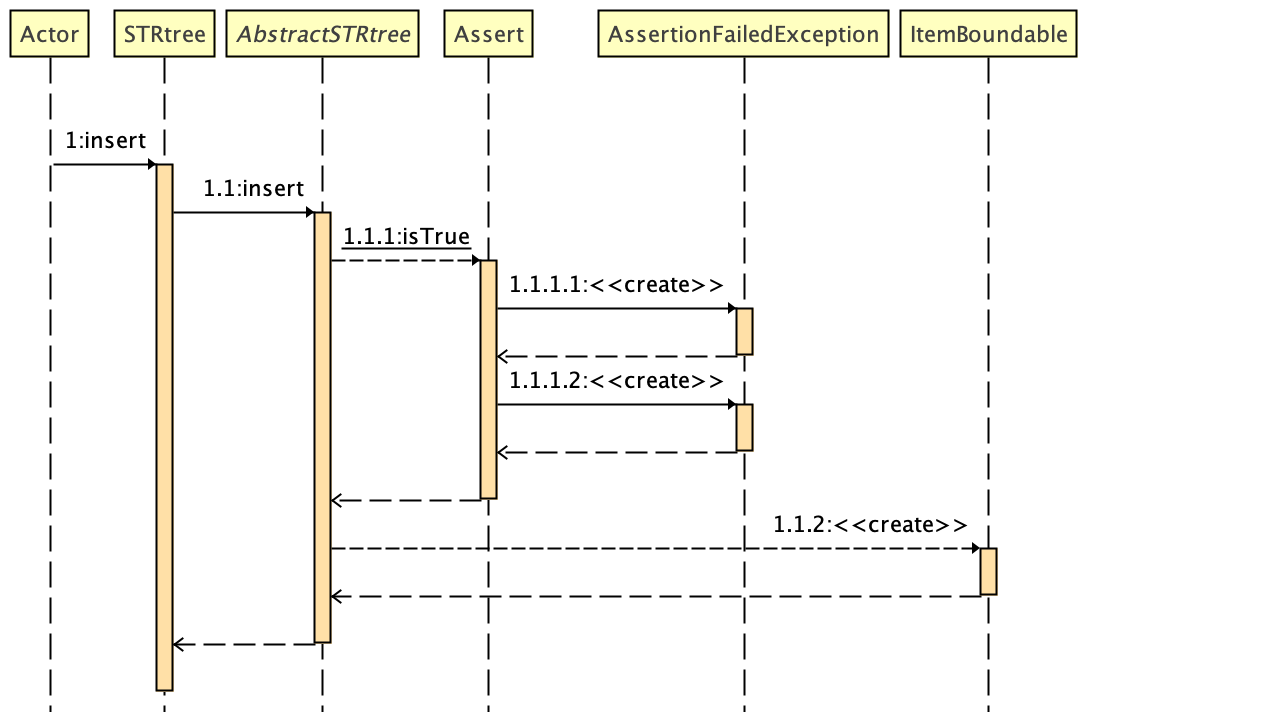
stRtree.insert(Envelope itemEnv, Object item)时序调用如下

  • 插入的一条记录为ItemBoundable 对象，包含一个Envelope和插入的数据
  • insert的数据实际就是叶子节点，RTree build的时候根据叶子节点向上构建。

STRtree_insert

Build

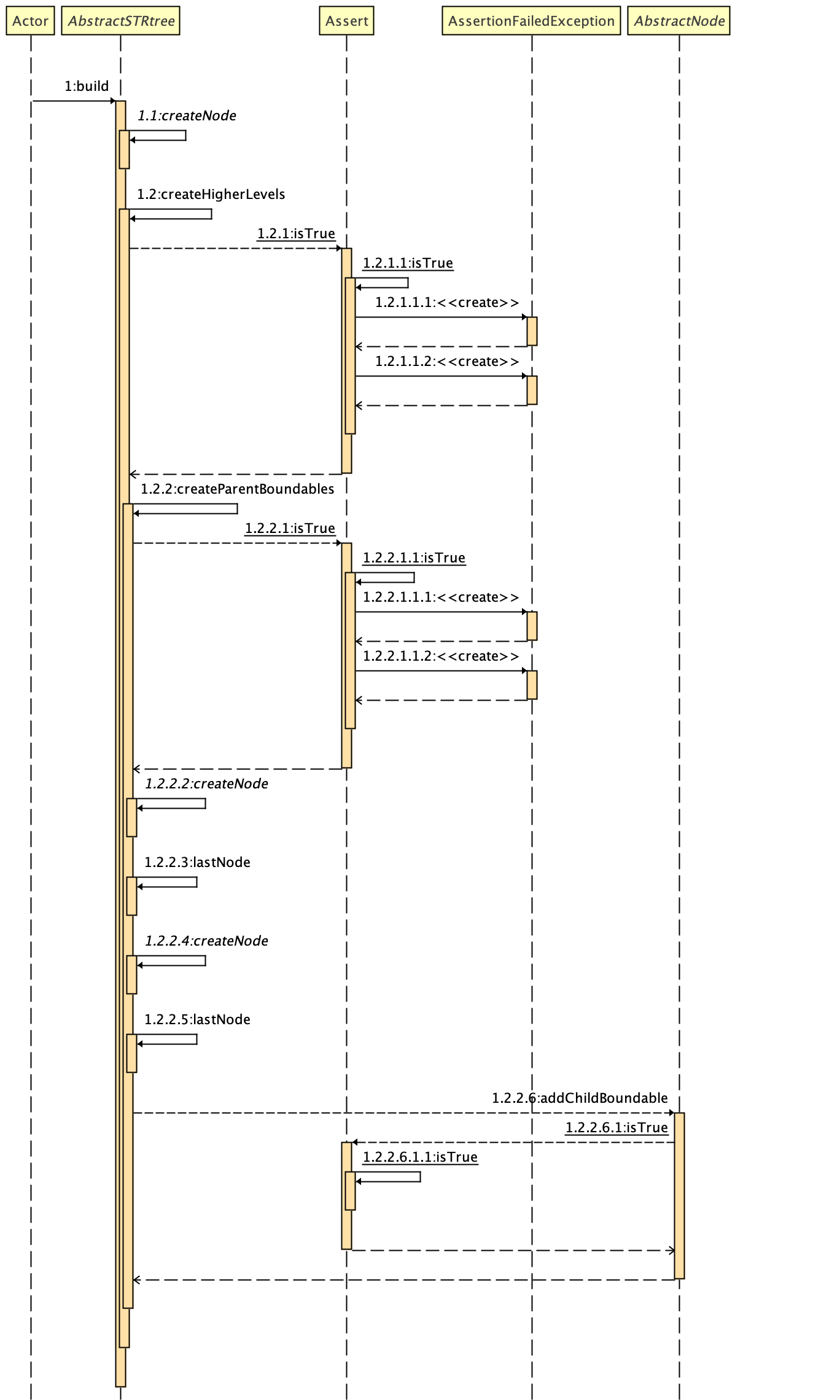
  • stRtree.build();真正构建R树

    • createHigherLevels递归构建R树，递归结束的条件就是父节点只有一个，即为根节点

      1
      2
      3
      4
      5
      6
      7
      8
      private AbstractNode createHigherLevels(List boundablesOfALevel, int level) {
        Assert.isTrue(!boundablesOfALevel.isEmpty());
        List parentBoundables = createParentBoundables(boundablesOfALevel, level + 1);
        if (parentBoundables.size() == 1) {
          return (AbstractNode) parentBoundables.get(0);
        }
        return createHigherLevels(parentBoundables, level + 1);
      }

    • createParentBoundables，根据给定的子节点信息，获取父节点的信息

      • GeoTool中STRtree对象每个节点的子节点默认大小为10个
      • 将子节点根据Envelope中心点按x轴排序，然后划分成 $\sqrt{r/n}$ 个slice，比如r=288, n=10，即划分为6个slice，每个slice包含288/6=48个节点
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      protected List createParentBoundables(List childBoundables, int newLevel) {
        Assert.isTrue(!childBoundables.isEmpty());
        int minLeafCount = (int) Math.ceil((childBoundables.size() / (double) getNodeCapacity()));
        ArrayList sortedChildBoundables = new ArrayList(childBoundables);
        Collections.sort(sortedChildBoundables, xComparator);
        List[] verticalSlices = verticalSlices(sortedChildBoundables,
            (int) Math.ceil(Math.sqrt(minLeafCount)));
        return createParentBoundablesFromVerticalSlices(verticalSlices, newLevel);
      }
          
      private List createParentBoundablesFromVerticalSlices(List[] verticalSlices, int newLevel) {
        Assert.isTrue(verticalSlices.length > 0);
        List parentBoundables = new ArrayList();
        for (int i = 0; i < verticalSlices.length; i++) {
          parentBoundables.addAll(
                createParentBoundablesFromVerticalSlice(verticalSlices[i], newLevel));
        }
        return parentBoundables;
      }
          
      protected List createParentBoundablesFromVerticalSlice(List childBoundables, int newLevel) {
        return super.createParentBoundables(childBoundables, newLevel);
      }

      • 其中super.createParentBoundables针对每个slice，按照y坐标排序，每10个节点划分到一个group中

        • 其中父节点使用的是createNode(newLevel)创建，创建的为AbstractNode对象，
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        19
        protected List createParentBoundables(List childBoundables, int newLevel) {
          Assert.isTrue(!childBoundables.isEmpty());
          ArrayList parentBoundables = new ArrayList();
          parentBoundables.add(createNode(newLevel));
          ArrayList sortedChildBoundables = new ArrayList(childBoundables);
          Collections.sort(sortedChildBoundables, getComparator());
          for (Iterator i = sortedChildBoundables.iterator(); i.hasNext(); ) {
            Boundable childBoundable = (Boundable) i.next();
            if (lastNode(parentBoundables).getChildBoundables().size() == getNodeCapacity()) {
              parentBoundables.add(createNode(newLevel));
            }
            lastNode(parentBoundables).addChildBoundable(childBoundable);
          }
          return parentBoundables;
        }
              
        protected AbstractNode lastNode(List nodes) {
          return (AbstractNode) nodes.get(nodes.size() - 1);
        }

        • 父节点的Envelope对象计算方式如下，即遍历父节点对应的子节点，找到能将子节点包围住的矩形框

          1
          2
          3
          4
          5
          6
          7
          8
          9
          10
          11
          12
          13
          14
          15
          16
          17
          18
          19
          20
          21
          22
          23
          24
          25
          26
          27
          28
          29
          30
          31
          32
          33
          34
          35
          36
          37
          38
          protected Object computeBounds() {
            Envelope bounds = null;
            for (Iterator i = getChildBoundables().iterator(); i.hasNext(); ) {
              Boundable childBoundable = (Boundable) i.next();
              if (bounds == null) {
                bounds = new Envelope((Envelope)childBoundable.getBounds());
              }
              else {
                bounds.expandToInclude((Envelope)childBoundable.getBounds());
              }
            }
            return bounds;
          }
            public void expandToInclude(Envelope other) {
              if (other.isNull()) {
                return;
              }
              if (isNull()) {
                minx = other.getMinX();
                maxx = other.getMaxX();
                miny = other.getMinY();
                maxy = other.getMaxY();
              }
              else {
                if (other.minx < minx) {
                  minx = other.minx;
                }
                if (other.maxx > maxx) {
                  maxx = other.maxx;
                }
                if (other.miny < miny) {
                  miny = other.miny;
                }
                if (other.maxy > maxy) {
                  maxy = other.maxy;
                }
              }
            }

image-20220327145347438

Query

  • 先判断根节点是否是否包含

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    protected List query(Object searchBounds) {
      build();
      ArrayList matches = new ArrayList();
      if (isEmpty()) {
        //Assert.isTrue(root.getBounds() == null);
        return matches;
      }
      if (getIntersectsOp().intersects(root.getBounds(), searchBounds)) {
        queryInternal(searchBounds, root, matches);
      }
      return matches;
    }

  • 然后递归查找子节点

    • 如上我们说的，insert的叶子节点是ItemBoundable对象，父节点是AbstractNode对象，根据此可以判断是否到达叶子节点
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
      
    private void queryInternal(Object searchBounds, AbstractNode node, List matches) {
      List childBoundables = node.getChildBoundables();
      for (int i = 0; i < childBoundables.size(); i++) {
        Boundable childBoundable = (Boundable) childBoundables.get(i);
        if (! getIntersectsOp().intersects(childBoundable.getBounds(), searchBounds)) {
          continue;
        }
        if (childBoundable instanceof AbstractNode) {
          queryInternal(searchBounds, (AbstractNode) childBoundable, matches);
        }
        else if (childBoundable instanceof ItemBoundable) {
          matches.add(((ItemBoundable)childBoundable).getItem());
        }
        else {
          Assert.shouldNeverReachHere();
        }
      }
    }

Reference

赏

谢谢你请我吃糖果

支付宝
微信

扫一扫，分享到微信

微信分享二维码
本站总访问量次 总访客数人次

tag:

    缺失模块。
    1、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    2、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: true
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

程序猿👨🏻‍💻